Research
| Line 361: | Line 361: | ||
| | | | ||
| + | <!-- | ||
{| style="margin-left: auto; margin-right: 0px; border:1px solid #abd5f5; background:#d0e5f5; padding:0.2em 0.5em; font-weight:bold;" | {| style="margin-left: auto; margin-right: 0px; border:1px solid #abd5f5; background:#d0e5f5; padding:0.2em 0.5em; font-weight:bold;" | ||
| Line 385: | Line 386: | ||
|} | |} | ||
|} | |} | ||
| + | --> | ||
|} | |} | ||
|} | |} | ||
Revision as of 09:26, 14 August 2016
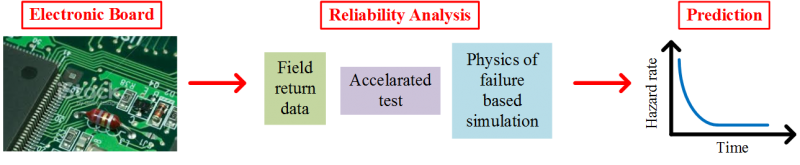
Our research aims to develop novel ways of computing, circuit design, and reliability for electronic circuits and systems. Our research mainly targets emerging technologies and new computing paradigms.
Contents |
Computing with Nano-Crossbar Arrays | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nano-crossbar arrays have emerged as a strong candidate technology to replace CMOS in near future. They are regular and dense structures, and fabricated by exploiting self-assembly as opposed to purely using lithography based conventional and relatively costly CMOS fabrication techniques. Currently, nano-crossbar arrays are fabricated such that each crosspoint can be used as a conventional electronic component such as a diode, a FET, or a switch. This is a unique opportunity that allows us to integrate well developed conventional circuit design techniques into nano-crossbar arrays. Motivated by this, we aim to develop a complete synthesis and performance optimization methodology for switching nano-crossbar arrays that leads to the design and construction of an emerging nanocomputer.
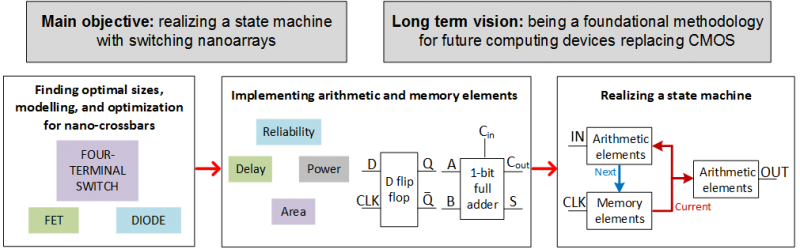 SynthesisWe study implementation of Boolean functions with nano-crossbar arrays where each crosspoint behaves as a diode, a FET, and a four-terminal switch. For these three types, we give array size formulations for a given Boolean function. Additionally, we focus on four-terminal switch based implementations and propose an algorithm that implements Boolean functions with optimal array sizes. Fault ToleranceWe examine reconfigurable crossbar arrays by considering randomly occurred stuck-open and stuck-closed crosspoint faults. In the presence of permanent faults, a fast and accurate heuristic algorithm is proposed that uses the techniques of index sorting, backtracking, and row matching. In the presence of transient faults, tolerance analysis is performed by formally and recursively determining tolerable fault positions
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reversible Circuit Design | ||||||||||||||||||||||||||||||||||
|
Unlike conventional logic gates, reversible logic gates do not have “don’t-care” conditions. It means that an error occurring in any node of a reversible circuit is always seen at the output that gives a unique opportunity for error detecting/correcting. Motivated by this, we implement error tolerant reversible circuit blocks by exploiting parity preserving logic and Hamming codes. We aim to design, fabricate, and test a fault-aware 8-bit reversible microprocessor for applications requiring high accuracy and reliability including aerospace, military, and medical applications. 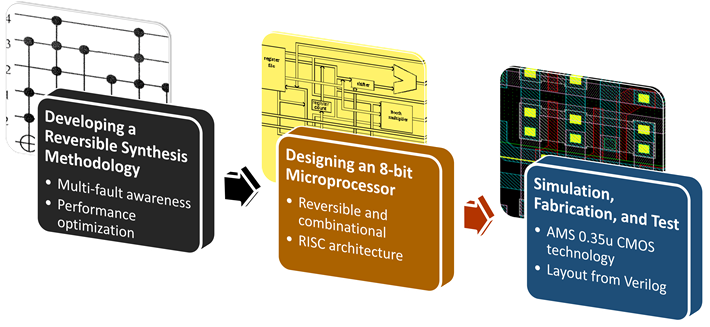 Synthesis and OptimizationWe propose a fast synthesis algorithm that implements any given reversible Boolean function with quantum gates. Instead of an exhaustive search on every given function, our algorithm creates a library of essential functions and performs sorting. As an example, to implement 4 bit circuits we only use 120 essential functions out of all 20922789888000 functions. We also perform optimization for both reversible and quantum circuit costs by considering adjacent gate pairs.
| ||||||||||||||||||||||||||||||||||
Stochastic Circuit Design | ||||||||||||||||||||||||||||||||||||||||||||||||||||
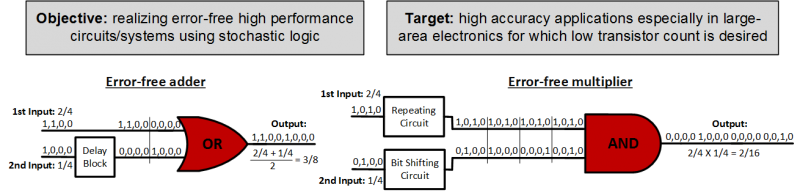
Accurate Arithmetic ImplementationsWe propose a method to overcome the main drawback in stochastic computing, low accuracy or related long computing times. Our method manipulates stochastic bit streams with the aid of feedback mechanisms. We implement error-free arithmetic multiplier and adder circuits by considering performance parameters area, delay, and accuracy.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||